KUNCI JAWABAN PERSOAL UN FISIKA KELAS XI

A. Dinamika rotasi
1. soal UN fisika 2015

jawaban : B

2. soal Un fisika 2015

jawaban : E
luas 1 = persegi panjang ( 4 x 8 = 32 m^2)
luas 2 = segitiga ( 1/2.4.6=12 m^2) jadi negatif karena yang tidak diarsir

y = 2.32 - 2.12 = 64-24=40
L = 32-12= 20

y = 40/20 =2

KUNCI JAWABAN PERSOAL UN FISIKA KELAS X

A. Pengukuran menggunakan alat ukur panjang, massa, dan waktu
1. soal UN 2015

Jawaban : C
skala utama = 2 mm
skala putar/nonius = 48 bagian x 0,01mm = 0,48 mm
--------------------------------- +
skala yg ditunjukan = 2,48 mm

Hukum Kepler I, II dan III

1. Hukum I Kepler
   Menjelaskan tentang bentuk lingkaran orbit planet. Bunyi hukum Keppler 1 berisi sebagai berikut.
   

   Lintasan setiap planet mengelilingi matahari merupakan sebuah elips dengan matahari terletak pada salah satu titik fokusnya.

   Nah setelah melihat hukum pertama Kepler dapat dilihat ilustrasi tersebut seperti pada Gambar berikut ini.
   
   Ilustrasi orbit planet sesuai hukum I Kepler
   
   
2. Hukum II Kepler
   Menjelaskan tentang kecepatan orbit planet. Apa perbedaan dengan hukum kepler pertama? Perhatikan penjelasan berikut, hukum Keppler 2 berisi sebagai berikut
   

   Setiap planet bergerak sedemikian sehingga suatu garis khayal yang ditarik dari matahari ke planet tersebut mencakup daerah dengan luas yang sama dalam waktu yang sama.

   Untuk lebih jelasnya silahkan amati gambar berikut
   
   

Sifat-Sifat Gelombang

Kelas XII

Setiap gelombang baik mekanik maupun elektromekanik memiliki sifat-sifat tertentu karena pada prinsipnya gelombang adalah rambatan dari energi getaran. Semuagelombang mekanik maupun gelombang elektromagnetik mempunyai sifat-sifat gelombang yang sama yaitu dapat dipantulkan (refleksi), dapat dibiaskan (refraksi), dapat saling berinterferensi (memadukan), dan mengalami difraksi (pelenturan), dispersi, dan polarisasi.

Sifat-Sifat Gelombang

Untuk mempelajari sifat pada gelombang dapat dilakukan kegiatan percobaan mengamati gelombang yang terjadi di permukaan air dengan menggunakan tangki riak atau tangki gelombang (ripple tank). Pada dasarnya tangki riak terdiri atas tangki air yang dasarnya terbuat dari kaca, motor listrik sebagai sumber getar yang diletakkan di atas papan penggetar dan akan menggetarkan papan penggetar yang berupa plat/keping untuk pembangkit gelombang lurus dan pembangkit berbentuk bola kecil untuk membangkitkan gelombang lingkaran. Sebuah lampu diletakkan di atas tangki riak untuk menyinari permukaan logam. Di bawah tangki riak diletakkan kertas putih untuk mengamati bentuk gelombang pada permukaan air. Puncak dan dasar gelombang akan terlihat pada kertas putih (layar) berupa garis gelap dan terang.

SOAL LATIHAN GELOMBANG

Nomor 1
Diberikan sebuah persamaan gelombang Y = 0,02 sin (10πt − 2πx) dengan t dalam sekon, Y dan x dalam meter.
Tentukan:

a. amplitudo gelombang
b. frekuensi sudut gelombang
c. tetapan gelombang
d. cepat rambat gelombang
e. frekuensi gelombang
f. periode gelombang
g. panjang gelombang
h. arah rambat gelombang
i. simpangan gelombang saat t = 1 sekon dan x = 1 m
j. persamaan kecepatan gelombang
k. kecepatan maksimum gelombang
l. persamaan percepatan gelombang
m. nilai mutlak percepatan maksimum
n. sudut fase saat t = 0,1 sekon pada x = 1/3 m
o. fase saat t = 0,1 sekon pada x = 1/3 m

Pembahasan :

Bentuk persamaan umum gelombang:

Y = A sin (ωt - kx)

dengan A amplitudo gelombang, ω = 2πf dan k = 2π/λ dengan demikian :

a. A = 0,02 m

b. ω = 10π rad/s
c. k = 2π
d. v = ω/k = 10π/2π = 5 m/s

e. f = ω/2π = 10π/2π = 5 Hz

f. T = 1/f = 1/ 5 = 0, 2 sekon

g. λ = 2π/k = 2π/2π = 1 m

h. ke arah sumbu x positif

i. Y = 0,02 sin(10 π- 2π) = 0,02 sin(8π) = 0 m
j. v = ω A cos(ωt−kx) = 10π(0,02) cos(10πt−2πx) m/s
k. vmaks = ωA = 10π(0,02) m/s
l. a = −ω2y = −(10π)2 (0,02) sin(10πt − 2πx) m/s2
m. amaks = |−ω2A| = |−(10π)2 (0,02)| m/s2
n. sudut fase θ = (10.π.0,1−2π.(1/3) = 1/3 π = 60o
o. fase φ = 60o/360o = 1/6

GEJALA GELOMBANG

A. Definisi

Gelombang didefinisikan sebagai getaran yang merambatkan energi dari satu tempat ketempat yang lain, baik melalui medium ataupun tidak. Gelombang air, gelombang tali, gelombang suara , gelombang elektromagnetik adalah contoh dari bebeapa gelombang.

Jenis jenis gelombang dapat dibedakan:

a. Berdasar Arah getar terhadap arah rambatnya:

• Gelombang Transversal: gelombang yang arah getarnya tegak lurus dengan rambatnya. Contohnya antara lain: gelombang tali, gelombang elektromagnetik cahaya.


• Gelombang Longitudinal: Gelombang lyang arah getanya searah dengan arah rambatnya. Contohnya adalah gelombang suara.

HUKUM GAYA GRAVITASI NEWTON 2

A. Perkembangan Teori Gravitasi

Sejak zaman Yunani Kuno, orang sudah berusaha menjelaskan tentang kinematika sistem tata surya. Oleh karena itu, sebelum membahas hukum gravitasi Newton, ada baiknya apabila Anda juga memahami pemikiran sebelum Newton menemukan hukum gravitasi. Plato (427 – 347 SM) ilmuwan yunani mengemukakan bahwa bintang dan bulan bergerak mengelilingi bumi membentuk lintasan lingkaran

sempurna. Claudius Ptolemaus pada abad ke-2 M juga memberikan pendapat yang serupa yang disebut teori geosentris. Teori ini menyatakan bumi sebagai pusat tata surya, sedangkan planet lain, bulan dan matahari berputar mengelilingi bumi. Namun, pendapat dari kedua tokoh tersebut

tidak dapat menjelaskan gerakan yang rumit dari planet-planet. Nicolaus Copernicus, ilmuwan asal Polandia, mencoba mencari jawaban yang lebih sederhana dari kelemahan pendapat Plato dan Ptolemaus. Ia

mengemukakan bahwa matahari sebagai pusat sistem planet dan planetplanet lain termasuk bumi mengitari matahari. Anggapan Copernicus memberikan dasar yang kuat untuk mengembangkan pandangan mengenai

tata surya. Namun, pertentangan pendapat di kalangan ilmuwan masih tetap ada. Hal ini mendorong para ilmuwan untuk mendapatkan data pengamatan yang lebih teliti dan konkret.

Tyco Brahe (1546–1601) berhasil menyusun data mengenai gerak planet secara teliti. Data yang Tyco susun kemudian dipelajari oleh Johannes Keppler (1571–1630). Keppler menemukan keteraturan-keteraturan gerak planet. Ia mengungkapkan tiga kaidah mengenai gerak planet, yang sekarang dikenal sebagai hukum I, II, dan III Kepler. Hukum-hukum Kepler tersebut menyatakan:

1. Semua planet bergerak di dalam lintasan elips yang berpusat di satu titik pusat (matahari).

2. Garis yang menghubungkan sebuah planet ke matahari akan memberikan luas sapuan yang sama dalam waktu yang sama.

3. Kuadrat dari periode tiap planet yang mengelilingi matahari sebanding dengan pangkat tiga jarak rata-rata planet ke matahari.

RESULTAN GAYA GRAVITASI

MENENTUKAN RESULTAN GAYA GRAVITASI METODE JAJAR GENJANG

Untuk mengetahui berapa besar gaya gravitasi yang bekerja pada suatu benda kita harus terlebih dahulu menguasai konsep penjumlahan vektor. Gaya adalah besaran vektor sehingga untuk menghitung resultan dari keseluruhan gaya dapat digunakan metode penjumlahan vektor seperti metode segitiga, poligon, jajargenjang, maupun penjumlahan sederhana dengan memperhatikan arah gaya-gayanya. Berikut beberapa bentuk kedudukan benda yang sering muncul dalam perhitungan resultan gaya gravitasi :

1. Benda A, B, dan C berada satu garis.

Benda A, B, dan C terletak pada satu garis lurus dimana B berada di antara A dan C. Jika mereka dipisahkan oleh jarak R, berapakah gaya total yang bekerja pada B ? ........

Read More>>

2. Benda A, B, dan C membentuk siku-siku, dimana B berada di siku-siku.

Jika garis yang menghubungkan benda A, B, dan C membentuk siku-siku dengan benda B berada pada siku-sikunya, maka untuk menghitung resultan gaya yang bekerja pada benda B digunakan metode segitiga (dalil pitagoras).........

3. Benda A, B, dan C membentuk sudut tertentu.

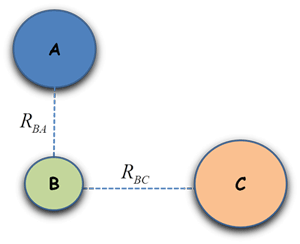
Jika benda A, B, dan C membentuk sudut tertentu dimana dalil pitagoral tidak berlaku, maka untuk menghitung resultan gaya yang bekerja pada benda B digunakan metode jajaran genjang. Adapun gaya-gaya yang bekerja pada benda B secara sederhana dilukiskan seperti gambar di bawah ini:

Keterangan :

Fba = gaya yang dialami benda B oleh benda A (N)

Fbc = gaya yang dialami benda B oleh benda C (N)

Rab = jarak antara benda B dan A diukur dari pusat benda A (m)

Rbc = jarak antara benda B dan C diukur dari pusat benda C (m)

Untuk menentukan resultan gaya gravitasi yang berarah sembarang seperti itu, maka digunakan metode jajaran genjang sehingga :

Fb = resultan gaya gravitasi yang bekerja pada benda B (N)

0 = sudut apit yang dibentuk oleh gaya yang mempengaruhi benda. (0< sudut apit< 180)

Cara Kerja Neraca Cavendish : Penentuan Konstanta G

MAR302014

Nilai tetapan semesta G yang sebelumnya tidak dapat ditentukan oleh Newton, ditentukan melalui percobaan yang dilakukan oleh seorang ilmuwan Inggris bernama Henry Cavendish pada 1798 dengan ketelitian sebesar 99%. Percobaan yang dilakukan Cavendish menggunakan sebuah neraca yang disebut Neraca Cavendish. Neraca tersebut dapat mengukur besar gaya putar yang diadakan pada lengan gayanya. Gambar berikut adalah sketsa dari peralatan Cavendish yang digunakan untuk mengukur gaya gravitasi antara dua benda kecil.

Neraca Cavendish dan Cara Kerjanya
Dua bola kecil, masing-masing dengan massa m1, diletakkan di ujung batang ringan yang digantungkan pada seutas tali halus. Di samping bola-bola kecil tersebut, digantungkan bola-bola besar dengan massa m2. Apabila tali penggantung massa m1dipuntir dengan sudut sebesar θ dan besar m2, m1, serta jarak antara kedua massa itu (d ) diketahui, besarnya G dapat dihitung.
Neraca Cavendish terdiri dari sebuah batang ringan yangdigantung pada bagian tengahnya oleh seutas serat kuarsa(kawat halus). Pada kefua ujung batang trdapat 2 bolatimbal kecil identik bermassa m dan diameternya kuranglebih 2 inci. Dua bola timbal besar identik bermassa M dandiameternya kira-kira 8 inci, dapat digerakkan sangat dekat(hampir bersentuhan) ke bola kecil m. gaya gravitasi (tarikmenarik) antara M dan m mentebabkan batang ringanterpuntir dan serat kuarsa berputar. Besarnya sudutpuntiran batang dideteksi dari pergeseran berkas cahayaskala.
Setelah sistem dikalibrasi sehingga besar gaya yangdiperlukan untuk menghasilkan suatu puntirantertentu diketahui, gaya tarik antara M dan m dapatdihitung secara langsung dari data pegamatan sudutpuntiranserat.mari kita susun persamaan berikut :
F = GMm/R2
Dengan nilai F ditentukan dari percobaan Cavendish,adalah masalah sederhana untuk mengukur massabola-bola timbal (m dan M)dan jarak antara keduanya(r) dari pusat ke pusat. Dengan diketahui semua nilaidari besaran-besaran pada ruas kanan, maka nilai Gdapat dihitung. Cavendish memperoleh nilai G=6,754X10-11 Nm2/kg2 dengan keakuratan 1% darinilai yang diterima saat ini, yaitu :G=6,672X10-16 Nm2/kg2
Beberapa metode dan alat ukur telah dikembangkan oleh para ilmuwan untuk mendapatkan nilai konstanta gravitasi yang lebih akurat. Walaupun G adalah suatu konstanta Fisika pertama yang pernah diukur, konstanta G tetap merupakan konstanta yang dikenal paling rendah tingkat ketelitiannya. Hal ini disebabkan tarikangravitasi yang sangat lemah sehingga dibutuhkan alat ukur yang sangat peka agar dapat mengukur nilai G dengan teliti. Hingga saat ini , nilai konstanta gravitasi universal G yang didapatkan oleh Cavendish, yaitu (6,70 ±0,48)× 10-11 Nm2/kg2 tidak jauh berbeda dengan nilai G yang didapat oleh para ilmuwan modern, yaitu 6,673 × 10-11 Nm2/kg2.
Penurunan Nilai Konstanta G
Penurunan persamaan untuk G dari percobaan ini cukup kompleks. Variabel yang diukur dalam percobaan adalah:
M adalah massa bola besar dalam kg
m adalah massa bola kecil di kg
R adalah pemisahan awal antara bola dalam meter
L adalah panjang bar keseimbangan dalam meter
θ (kecil huruf Yunani omega) adalah sudut dari posisi diam ke titik ekuilibrium diukur dalam radian
T adalah periode osilasi dalam hitungan detik
Persamaan umum gravitasi adalah :
F = GMm/R2
dimana
F adalah gaya tarik-menarik antara bola dalam newton (N)
G adalah Konstan Gravitasi Universal di dalam N-m2/kg2 atau m3/kg-s2
Pemecahan untuk G:
G = FR2/Mm

Gaya terkait dengan torsi
Kekuatan F berhubungan dengan torsi pada serat. Persamaan untuk torsi adalah gaya yang diterapkan kali lengan momen. Karena ada dua lengan saat L / 2, torsi adalah:
τ = FL
di mana τ (kecil huruf Yunani tau) adalah torsi dalam Nm. Dengan demikian:
F = τ / L

Torsi yang berkaitan dengan koefisien torsi
Namun, torsi juga terkait dengan koefisien torsi dari serat atau kawat:
τ = κθ
di mana κ (kappa kecil huruf Yunani) adalah koefisien torsi di newton-meters/radian. Dengan demikian:
F = κθ / L

Koefisien torsi yang berhubungan dengan periode osilasi
Yang belum diketahui adalah faktor koefisien torsi, yang dihitung dengan mengukur periode osilasi resonansi kawat.
Ketika bar keseimbangan awalnya dilepaskan dan bola bergerak mendekati bola besar, inersia yang lebih kecil menyebabkan mereka melampaui sudut keseimbangan. Hal ini menyebabkan keseimbangan torsi berosilasi kembali pada periode osilasi resonansi alami:
T = 2π √ (I / κ)
dimana
T adalah periode osilasi dalam hitungan detik
π (kecil huruf Yunani pi) 3.14 …
I adalah momen inersia bola kecil dalam kg-m2
Catatan: massa bar dianggap diabaikan dan bukan faktor dalam inersia.

Periode Osilasi yang terkait dengan momen inersia
Momen inersia dari bola kecil adalah:
I = ML2 / 2
Pengganti inersia dalam persamaan torsi:
T = 2π √ (mL2/2κ)
Memecahkan κ:
T2 = 4π2(mL2/2κ)
2κT2 = 4π2mL2
κ = 2π2mL2/T2
Pengganti κ dalam persamaan untuk F:
F = κθ / L
Dengan demikian:
F = 2π2mL2θ/LT2
Mencari Nilai Konstanta G
Menggantikan F dalam persamaan untuk G:
G = FR2/Mm
G = 2π2mL2θR2/LT2Mm
Menyederhanakan persamaan:
G = 2π2LθR2/T2M
Nilai yang dihitung dari G dari penelitian ini adalah:
G = 6.674*10−11 m3/kg-s2
Karena newton setara dengan kg-m/s2, G juga didefinisikan sebagai:
G = 6.674*10−11 N-m2/kg2

HUKUM GRAVITASI NEWTON

HUKUM GRAVITASI NEWTON

Jika malam telah tiba, perhatikanlah bulan di langit! Apakah bulan dalam keadaan diam?

Mengapa bulan tidak jatuh ke bumi? Perhatikan pula sebuah pohon di sekitarmu! Apakah ada daun yang jatuh di bawah pohon? Meng apa daun yang massanya ringan dapat jatuh ke per mukaan bumi, sedangkan bulan yang massa nya jauh lebih besar dibanding selembar daun tidak jatuh ke bumi? Jawaban atas pertanyaan-pertanyaan tersebut akan kita bahas pada bab ini.

Kata Kunci: Gaya Gravitasi – Medan Gravitasi – Hukum Kepler – Hukum Newton – Penerapan

A. Gravitasi

     Pada abad XVI Masehi, Newton mengemukakan bahwa ada suatu ”gaya pada suatu jarak” yang memungkinkan dua benda atau lebih saling berinteraksi. Istilah tersebut oleh Michael Faraday, pada abad XVIII diubah menjadi istilah medan. Medan adalah tempat di sekitar suatu besaran fisik yang masih dipengaruhi oleh besaran tersebut dalam suatu satuan tertentu. Sebagai contoh, gaya gravitasi akan bekerja pada massa suatu benda yang masih berada dalam medan gravitasi suatu benda atau planet. Jika medan gravitasi sudah dapat diabaikan maka sebuah massa

yang berada di sekitar besaran benda tersebut tidak dapat dipengaruhi. Dengan demikian, dapat diketahui, meng apa daun yang massanya lebih kecil dibanding bulan yang massanya jauh lebih besar dapat ditarik oleh bumi. Berikut ini akan kita pelajari lebih jauh tentang gaya gravitasi.

1. Gaya Gravitasi

 Gambar 2.3 Sir Isaac Newton 

Isaac Newton dilahirkan di Inggris pada tahun 1642. Newton berhasil menemukan kalkulus dan teori gravitasi. Konon, teori gravitasi yang ditemukan Newton diilhami dari peristiwa jatuhnya buah apel yang dilihatnya. Ia heran mengapa buah apel jatuh ke bawah dan bukan ke atas. Newton meninggal pada usia 85 tahun (tahun 1727).

Dalam penelitiannya, Newton menyimpulkan bahwa gaya gravitasi atau gaya tarik-menarik antara dua benda dipengaruhi jarak kedua benda tersebut, sehingga gaya gravitasi bumi berkurang sebanding dengan kuadrat jaraknya. Bunyi hukum gravitasi Newton adalah setiap partikel di alam semesta ini akan mengalami gaya tarik satu dengan yang lain. Besar gaya tarik-menarik ini berbanding lurus dengan massa masing-masing benda dan berbanding terbalik dengan kuadrat jarak antara keduanya.

Secara matematis, hukum gravitasi Newton dapat dirumuskan sebagai berikut:

Keterangan:

F : gaya tarik-menarik antara kedua benda (N)

M₁ : massa benda 1 (kg)

m₂ : massa benda 2 (kg)

r  : jarak kedua benda (m)

G : tetapan gravitasi

    Pada persamaan 2.1 muncul konstanta G. Konstanta ini menunjuk kan nilai tetapan gravitasi bumi. Penentuan nilai G per tama kali dilakukan oleh Henry Cavendish dengan menggunakan neraca torsi. Neraca ter sebut kemudian dikenal dengan neraca Cavendish. Pada neraca Cavendish terdapat dua buah bola dengan massa berbeda, yaitu m dan M.

Perhatikan gambar 2.2 di samping! Kedua bola pada gambar 2.2 dapat bergerak bebas pada  poros dan tarik-menarik, sehingga akan memuntir serat kuarsa. Hal ini menyebabkan cahaya yang memantul pada cermin akan bergeser pada skala. Setelah meng konversi skala dan memerhatikan jarak m dan M serta massa m dan M, Cavendish menetapkan nilai G sebesar 6,754 × 10-11 N.m2/kg2. Nilai tersebut kemudian disempurnakan menjadi:

G = 6,672 × 10^-11 N.m² /kg².

Gaya gravitasi merupakan besaran vektor. Apabila suatu benda mengalami gaya gravitasi dari dua atau lebih benda sumber gravitasi maka teknik mencari resultannya menggunakan teknik pencarian resultan vektor.

Dalam bentuk vektor gaya gravitasi dirumuskan:

  

  2. Medan Gravitasi

Sebagaimana telah kita singgung pada awal bab ini bahwa benda akan tertarik oleh gaya gravitasi benda lain atau planet jika benda tersebut berada dalam pengaruh medan gravitasi. Medan gravitasi ini akan menunjukkan besarnya percepatan gravitasi dari suatu benda di sekitar benda lain atau planet. Besar medan gravitasi atau percepatan gravitasi dapat dirumuskan sebagai berikut.

Keterangan:

g : medan gravitasi atau percepatan gravitasi (m/s²)

G : tetapan gravitasi (6,672 × 10-11 N.m²/kg²)

M : massa dari suatu planet atau benda (kg)

r : jarak suatu titik ke pusat planet atau pusat benda (m)

Hal yang perlu diperhatikan dalam membahas medan gravitasi atau percepatan gravitasi adalah konsep bahwa massa benda dan berat benda tidaklah sama. Massa benda di mana pun tetap, namun berat benda di berbagai tempat belum tentu sama atau tetap. Besar percepatan gravitasi yang dialami semua benda di permukaan planet adalah sama. Jika selembar kertas jatuh ke tanah lebih lambat dari sebuah kelereng, bukan disebabkan karena per cepatan gravitasi di tempat tersebut berbeda untuk benda yang berbeda. Hal ini disebabkan oleh adanya hambatan udara yang menahan laju kertas tersebut. 

Hukum Newton juga menunjukkan bahwa pada umumnya jika sebuah benda (misalnya planet) bergerak mengelilingi pusat gaya (misalnya matahari), benda akan ditarik oleh gaya yang berubah sebanding dengan . Lintasan benda tersebut dapat be rupa elips, parabola, atau hiperbola.

Hukum gravitasi Newton juga dapat diterapkan pada gerak benda-benda angkasa. Sebelum masuk ke penerapan tersebut, kita pelajari terlebih dahulu tentang pergerakan benda-benda angkasa. Pergerakan benda-benda angkasa telah dipelajari oleh Johanes Kepler dan dinyatakan dalam hukum-hukum Kepler.

B. Hukum-hukum Newton tentang Gerak

Selain hukum gravitasi, Newton juga mengembangkan tiga hokum tentang gerak yang menjelaskan bagaimana gaya menyebabkan benda bergerak. Semua hukum Newton ini sering disebut fisika klasik. Berikut ini akan kita pelajari ketiga hukum Newton tersebut.

1. Hukum I Newton

Sebuah benda akan tetap diam jika tidak ada gaya yang bekerja padanya. Demikian pula sebuah benda akan tetap bergerak lurus beraturan (kecepatan benda tetap) jika gaya atau resultan gaya pada benda adalah nol. Pernyataan ini dirumuskan menjadi hukum I Newton yang berbunyi sebagai berikut. Sebuah benda akan tetap diam atau tetap bergerak lurus beraturan jika tidak ada resultan gaya yang bekerja pada benda itu.

Coba perhatikan gambar 2.7 di samping! Pada gambar 2.7 benda dalam keadaan diam karena gaya dorong, gaya gesek, gaya berat, gaya normal pada benda setimbang. Dengan kata lain, benda tersebut diam karena resultan gaya pada benda = 0.

Sebagai contoh, sebuah batu besar di lereng gunung akan tetap diam di tempatnya sampai ada gaya luar lain yang memindahkannya. Misalnya ada gaya tektonis/gempa atau gaya mesin dari buldoser. Demikian pula, bongkahan batu meteor di ruang angkasa akan terus bergerak selamanya dengan kecepatan tetap sampai ada gaya yang mengubah kecepatannya. Misalnya batu meteor itu bertumbukan dengan meteor lain.

Jadi, jika resultan dari gaya-gaya yang bekerja pada sebuah benda sama dengan nol (S F = 0)

maka percepatan benda juga sama dengan nol (a = 0). Dengan demikian:

a. Jika benda dalam keadaan diam maka benda akan tetap diam, atau

b. Jika benda dalam keadaan bergerak lurus beraturan maka benda akan tetap bergerak lurus beraturan.

Benda akan selalu berusaha mempertahankan keadaan awal jika benda tidak dikenai gaya atau resultan gaya. Hal ini yang menyebabkan hukum I Newton disebut sebagai hukum kelembaman/ inersia (malas/inert untuk berubah dari keadaan awal). Dalam persamaan

matematis, hukum I Newton adalah sebagai berikut.

SF = 0 . . . (2.10)

Keterangan:

S F : resultan gaya yang bekerja pada benda (N)

Jika benda bergerak lurus beraturan atau diam pada sistem koordinat kartesius, persamaan 2.10 menjadi

S Fx = 0 dan SFy = 0 . . . (2.11)

Dengan demikian dapat disimpulkan bahwa jika SF = 0 maka benda tidak mengalami percepatan (a = 0). Jika digambarkan dalam koordinat kartesius,

gaya-gaya yang bekerja pada benda diam atau bergerak lurus beraturan dapat kita lihat pada gambar 2.8.

2. Hukum II Newton

        Apabila resultan gaya yang timbul pada sebuah benda tidak sama dengan nol maka benda tersebut akan bergerak dengan percepatan tertentu. Perhatikan gambar 2.9 di samping! Sebuah benda bermassa mmendapat gaya F akan bergerak dengan percepatan a. Jika benda semula

dalam keadaan diam maka benda itu akan bergerak dipercepat dengan percepatan tertentu. Adapun jika benda semula bergerak dengan kecepatan tetap maka benda akan berubah menjadi gerak dipercepat atau diperlambat.

Resultan gaya yang bekerja pada benda bermassa konstan setara dengan hasil kali massa benda dengan percepatan nya. Pernyataan ini dikenal sebagai hukum II Newton dan dapat dirumuskan sebagai berikut

S F = m . a . . . (2.12)

Keterangan:

m : massa benda (kg)

a : percepatan benda (m/s2)

3. Hukum III Newton

Ketika kamu mendorong dinding, sesungguhnya pada saat yang sama dinding tersebut memberikan gaya yang sama ke arahmu.

Kerja Mandiri 2

Bagaimana hal ini terjadi?

Kenyataan ini dikemukakan oleh Newton dalam hukumnya yang ketiga sebagai berikut. Jika benda pertama me ngerjakan gaya pada benda kedua maka benda kedua juga akan mengerjakan gaya pada benda. pertama yang besarnya sama, tetapi berlawanan arah. Hukum III Newton juga dikenal sebagai hokum aksi-reaksi. Secara matematis hokum III Newton dapat dituliskan sebagai berikut.

sebagai berikut

S F = m . a . . . (2.12)

Keterangan:

m : massa benda (kg)

a : percepatan benda (m/s2)

3. Hukum III Newton

Ketika kamu mendorong dinding, sesungguhnya pada saat yang sama dinding tersebut memberikan gaya yang sama ke arahmu.

Kerja Mandiri 2

Bagaimana hal ini terjadi?

Kenyataan ini dikemukakan oleh Newton dalam hukumnya yang ketiga sebagai berikut. Jika benda pertama me ngerjakan gaya pada benda kedua maka benda kedua juga akan mengerjakan gaya pada benda. pertama yang besarnya sama, tetapi berlawanan arah. Hukum III Newton juga dikenal sebagai hokum aksi-reaksi. Secara matematis hokum III Newton dapat dituliskan sebagai berikut.

Faksi = -Freaksi . . . (2.13)

Gaya aksi-reaksi terjadi pada dua benda yang berbeda, bukan pada satu benda yang sama. Sebagai contoh, gaya berat dan gaya normal pada sebuah buku yang tergeletak di meja

bukan merupakan pasangan gaya aksireaksi

C. Penerapan Hukum Gravitasi Newton pada

Benda-benda Angkasa

Hukum gravitasi Newton berlaku untuk semua benda, termasuk benda-benda angkasa. Jika ada dua buah benda angkasa atau lebih berinteraksi maka benda-benda tersebut akan tarikmenarik (bekerja gaya gravitasi). Gaya gravitasi menyebabkan bumi dan planet-planet dalam tata surya kita tetap mengorbit pada matahari. Gaya gravitasi antara bulan dan bumi me nyebabkan terjadinya pasang surut air laut dan berbagai macam fenomena alam. Berikut ini merupa kan contoh penerapan hukum gravitasi Newton pada benda-benda angkasa.

1. Gaya antara Matahari dan Planet

Gaya yang muncul akibat interaksi antara matahari dengan planet bukan hanya gaya gravitasi. Pada sistem tersebut juga bekerja gaya sentripetal (Fs) yang arahnya menuju pusat orbit planet. Gaya sentripetal dapat dirumuskan sebagai berikut.

 

Keterangan:

Fs : gaya sentripetal (N)

m : massa planet (kg)

v : kelajuan planet mengorbit matahari (m/s)

R : jarak matahari ke planet (km)

Dengan menggunakan persamaan 2.1 dan 2.14, massa matahari dapat ditentukan dengan rumus

Keterangan:

M : massa matahari (kg)

Jika kita asumsikan bahwa lintasan planet mengelilingi matahari berbentuk lingkaran, kelajuan planet mengitari matahari adalah:

2. Gaya pada Satelit

        Sebelumnya telah dijelaskan bahwa interaksi antara matahari dan planet akan menimbulkan gaya gravitasi dan gaya sentripetal. Prinsip yang sama juga berlaku untuk satelit yang mengorbit pada planet. Misalnya sebuah satelit mengitari planet dengan orbit berbentuk lingkaran. Gaya sentripetal yang dialami satelit berasal dari gaya gravitasi planet yang bekerja pada satelit tersebut. Besarnya kelajuan satelit mengitari planet dapat diketahui dengan rumus berikut.

Keterangan:

m_s : massa satelit (kg)

r : jarak antara pusat planet dengan satelit (km)

v_s : kelajuan satelit (m/s)